筆者は(一応)文系なので、数学的な記法、特に集合に関する記法については誤りを含んでいる可能性があります。
ニュアンスで汲み取ってください。
致命的な誤用がある場合はコメントやツイッターで教えてほしいです。
問題概要
$ 2N $ 個のピースからなる円形のケーキにいちごを乗せる。
ピース $ [ i , \, i+N ) $ には合計 $ A _ i $ 個以上のいちごを乗せる必要があるとき、ケーキ全体に乗せるべきいちごの数の最小値を求めよ。
https://atcoder.jp/contests/arc117/tasks/arc117_f
証明パートも含めるとかなり長くなるので、何をするのか簡潔に記しておく。
- $ A _ {2N-1} $ が最大値となるようにケーキを回転させる
- $ [ N , \, 2N ) $ に正のいちごを乗せる操作を $ [ 0 , \, N ) $ に負のいちごを乗せる操作とみなす
- $ A _ {i} = A _ {2N-1} \, ( N-1 \leqq i < 2N-1 ) $ となるよう $ [ 0 , \, N ) $ にいちごを乗せる
- $ max \, A _ {i} = A _ {2N-1} \, ( 0 \leqq i < N-1 ) $ となるようピース $ 0 $ に正のいちごを乗せる
- 負のいちごの総数が $ A _ {2N-1} $ 以下になるまでいちごを取り除く
- $ 2A _ {2N-1} - ( $ 負のいちごの総数 $ ) + ( $ 正のいちごの総数 $ ) $ が求める値
1. ケーキの回転
回転させても問題ないことは明らか。
ついでに配列 $ A $ も回転させて、条件文を「ピース $ [ i , \, i+N ) $ には合計 $ A _ {i+N-1} $ 個以上のいちごを乗せる」と言い換えておく。
2. 負のいちごを乗せる
ピース $ i $ にいちごを $ x $ 個乗せる操作を「 $ a \in \lbrace A _ {k} \mid i \leqq k < i+N \rbrace $ を満たす全ての $ a $ を $ -x $ する効果がある」という意味で $ d _ {i} = -x $ と表すこととする。
また、$ d _ {i} $ の連続 $ N $ 個の和を $ S _ {i+N-1} = \left( \sum _ {k=i} ^ {i+N-1} d _ {k} \right) $ とおく。
すると、満たすべき条件は
$$ \begin{gather}
A _ {i+N-1} + S _ {i+N-1} \leqq 0 \notag \\
\Leftrightarrow A _ {i} + S _ {i} \leqq 0
\end{gather} $$
と表すことができる。
$ i = 2N-1 $ のとき、$ (1) $ より
$$ A _ {2N-1} + S _ {2N-1} \leqq 0 $$
である(下図は $ N = 3 $ のとき)。
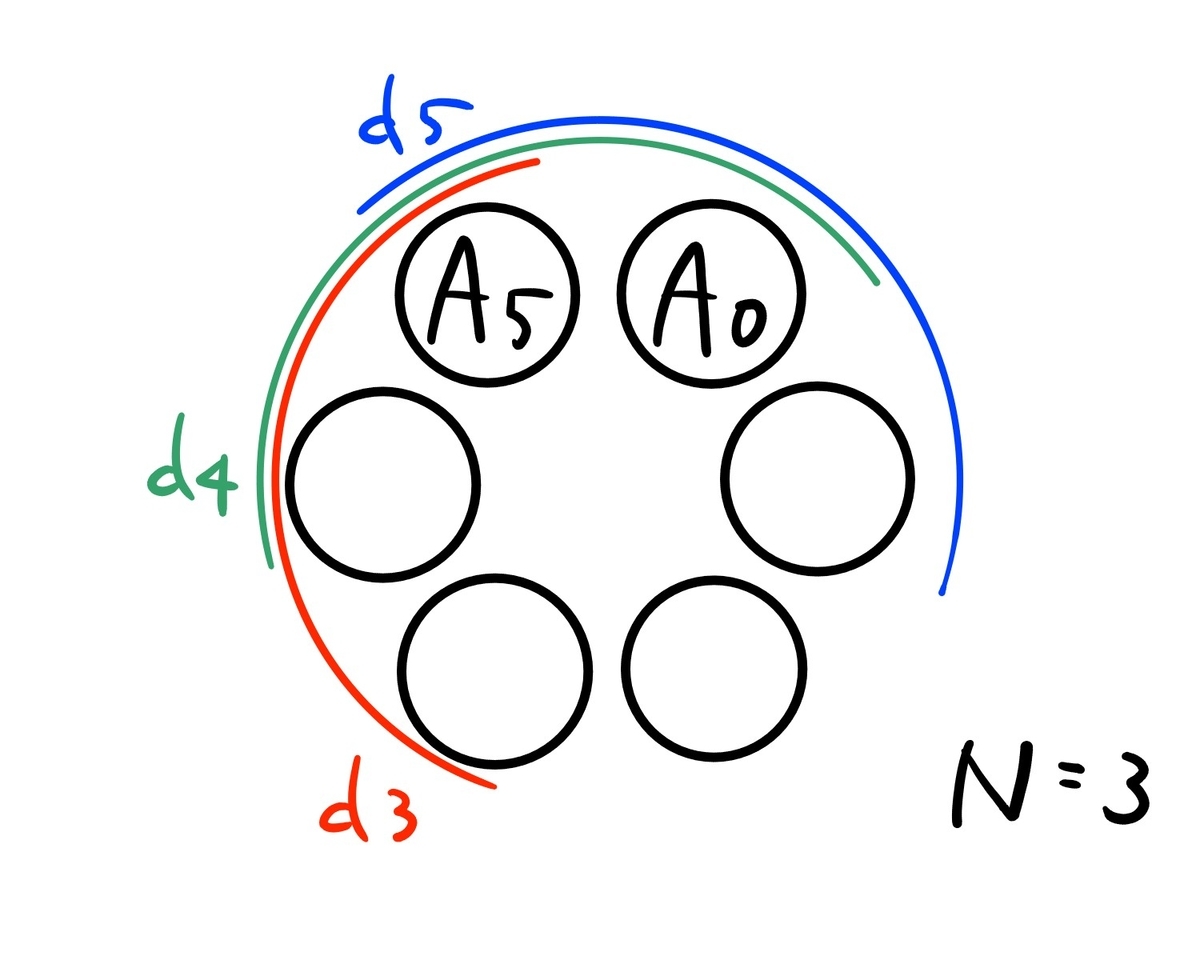
さて、$ A _ {2N-1} + S _ {2N-1} < 0 $ かつ $ d _ {2N-1} < 0 $ である限り、$ d _ {2N-1} $ に含まれる $ -1 $ を $ d _ {0} $ へ移動することができる。
元の言い方に即して言うと、ピース $ 2N-1 $ に乗っていたいちご $ 1 $ 個をピース $ 0 $ に移動できる $ ( * ) $ 。
(この操作を行うことによって悪影響があるのは $ A _ {2N-1} $ だけであり、操作後も $ (2) $ を満たしている。また、いちごの総数も変わらない。)

また、$ d _ {2N-1} = 0 $ のときは、$ A _ {2N-2} \leqq A _ {2N-1} $ かつ $ S _ {2N-2} = S _ {2N-1} - d _ {2N-1} + d _ {N-1} \leqq S _ {2N-1} $ より
$$ A _ {2N-2} + S _ {2N-2} < 0 \notag $$
となるため、先ほどと同様に $ d _ {2N-2} $ から $ d _ {2N-1} $ へ移動することができ、さらに $ d _ {0} $ へ移動できる。
この操作を繰り返すと、
$$ A _ {2N-1} + S _ {2N-1} = 0 $$
となり、すなわち「ピース $ [ N , \, 2N ) $ には合計 $ A _ {2N-1} $ 個ちょうどのいちごが乗っている」状態にできる。
以降、$ (3) $ が常に成り立っているものとする。
ここで、一旦 $ d _ {i} , \, d _ {i+N} $ をともに $ -d _ {i+N} $ することを考える。
この操作を $ [ 0, \, N ) $ で行うと、
$$ \hat{d} _ {i} = \left\{ \begin{align}
& d _ {i} - d _ {i+N} & & ( 0 \leqq i < N ) \notag \\
& 0 & & ( N \leqq i < 2N ) \notag
\end{align} \right. $$
と変形できる。
そして、$ \hat{S} _ {i+N-1} = \left( \sum _ {k=i} ^ {i+N-1} \hat{d} _ {k} \right) $ とすると、$ \hat{S} _ {i} = S _ {i} - S _ {2N-1} $ であるから、$ (1) \, (3) $ より
$$ \begin{gather}
A _ {i} + \hat{S} _ {i} + S _ {2N-1} \leqq 0 \notag \\
\Leftrightarrow \hat{S} _ {i} \leqq A _ {2N-1} - A _ {i}
\end{gather} $$
を満たすように $ \hat{D} = \lbrace \hat{d} _ {i} \rbrace $ を構築すればよい。
6. 最終目標
ナンバリングは前後するが、求めるべき最小値について先に整理しておく。
$$ \begin{align}
ans & = min \, ( - \sum _ {k=0} ^ {2N-1} d _ {k} ) \notag \\
& = min - ( S _ {2N-1} + S _ {N-1} ) \notag \\
& = min - ( 2S _ {2N-1} + \hat{S} _ {N-1} ) \notag \\
& = 2A _ {2N-1} - max \, \hat{S} _ {N-1}
\end{align} $$
つまり、$ (4) $ を満たすようにして $ \hat{S} _ {N-1} = \sum \hat{d} _ {k} $ を最大化すればよい。
3. $ [ N-1, \, 2N ) $ の条件を満たす
$ i = 2N-1 $ においては当然 $ (4) $ を満たしている。
各 $ \hat{d} _ {i} $ を最大化するには、$ (4) $ より
$$ \hat{S} _ {i} = A _ {2N-1} - A _ {i} \qquad ( N-1 \leqq i < 2N-1 ) $$
であればよい。

$$ \begin{flalign}
\hat{d} _ {N-1} & = \hat{S} _ {2N-2} - \hat{S} _ {2N-1} = A _ {2N-1} - A _ {2N-2} & \notag \\
\hat{d} _ {N-2} & = \hat{S} _ {2N-3} - \hat{S} _ {2N-2} = A _ {2N-2} - A _ {2N-3} & \notag \\
\hat{d} _ {N-3} & = \hat{S} _ {2N-4} - \hat{S} _ {2N-3} = A _ {2N-3} - A _ {2N-4} & \notag \\
& \quad \vdots & \notag \\
\hat{d} _ {0} & = \hat{S} _ {N-1} - \hat{S} _ {N} = A _ {N} - A _ {N-1} & \notag
\end{flalign} $$
これでひとまずピース $ [ N-1 , \, 2N) $ については $ (4) $ を満たしている。
4. $ \hat{d} _ {0} $ を減少させる
ピース $ [ 0 , \, N-1 ) $ については $ (4) $ の条件を満たしていないことがある。
$ (6) $ を用いて
$$ \begin{align}
(4) & \Leftrightarrow A _ {i} + \hat{S} _ {i} \leqq A _ {2N-1} \notag \\
& \Leftrightarrow A _ {i} + ( \hat{S} _ {N-1} - \hat{S} _ {i+N} ) \leqq A _ {2N-1} \notag \\
& \Leftrightarrow A _ {i} + ( A _ {i+N} - A _ {N-1} ) \leqq A _ {2N-1} \notag \\
& \Leftrightarrow A _ {i} + A _ {i+N} \leqq A _ {N-1} + A _ {2N-1} \qquad ( 0 \leqq i < N-1 ) \notag
\end{align} $$
であるから、$ max \, ( A _ {i} + A _ {i+N} ) - ( A _ {N-1} + A _ {2N-1} ) $ の値を $ \hat{d} _ {0} $ から減少させておく必要がある。
ここで、「 $ \hat{d} _ {0} $ から減少させる」必要性はないが、 $ ( * ) $ と同様の議論によって「 $ \hat{S} _ {i} < A _ {2N-1} - A _ {i} $ かつ $ \hat{d} _ {i} < 0 $ である限り、$ \hat{d} _ {i} $ から $ \hat{d} _ {i+1} $ へ転嫁できる(以降、「転嫁操作」と呼ぶ)」ことがわかる。
すなわち、とりあえず $ \hat{D} $ の先頭要素である $ \hat{d} _ {0} $ から減らしておけば必要以上に不利益を被ることはない。
5. $ \hat{d} _ {i} $ を調整する
当初 $ \hat{D} $ は、$ \lbrace d _ {i} \rbrace $ から $ [ N , \, 2N ) $ の範囲を $ [ 0 , \, N ) $ に反転させることで構築した。
$ d _ {i} \leqq 0 $ であるから、$ P = \lbrace x \in \hat{D} \mid x > 0 \rbrace $ とすると、
$$ \left( \sum _ { x \in P } x \right) \leqq - S _ {2N-1} = A _ {2N-1} $$
が条件である。
この条件を満たさない場合、任意の $ \hat{d} _ {i} \in P $ を減少させなければならない。
さて、$ [ 0 , \, N-1 ) $ において転嫁操作を行えなくなるまで繰り返したとき、$ 0 \leqq \hat{S} _ {i} \leqq \hat{S} _ {N-1} $ となる。
少し雑な証明
$ N-1 \leqq i $ については $ (6) $ から常に成立するので、$ i < N-1 $ についてのみ証明する。
$ \hat{S} _ {i} < 0 $ を満たす $ i $ が存在すると仮定する。
そのような $ i $ には $ \hat{d} _ {i} < 0 $ となるものが必ず存在する。
また、$ \hat{S} _ {i} < 0 \leqq A _ {2N-1} - A _ {i} $ となるため、転嫁操作を追加で行うことができ、「もう転嫁操作を行えない」という条件に反する。
したがって、$ 0 \leqq \hat{S} _ {i} $ は常に成立する。
$ \hat{S} _ {i} > \hat{S} _ {N-1} $ を満たす $ i $ が存在すると仮定する。
$ \hat{S} _ {i} + \hat{S} _ {i+N} = \hat{S} _ {N-1} $ より $ \hat{S} _ {i+N} < 0 $ となる。
しかし、$ (6) $ より $ \hat{S} _ {i+N} = A _ {2N-1} - A _ {i+N} \geqq 0 $ であったはずなので、$ \hat{d} _ {i-1} $ から $ \hat{d} _ {i} $ への転嫁操作が行われたことになる。
すると、その転嫁操作の前は $ \hat{d} _ {i-1} < 0 $ であり、$ \hat{S} _ {i+N-1} = \hat{d} _ {i-1} + \hat{S} _ {i+N} < 0 $ となって、同様の議論によって $ \hat{d} _ {i-2} $ から $ \hat{d} _ {i-1} $ への転嫁操作が行われたことになる。
これを繰り返すと、全ての $ j \, ( < i ) $ について $ \hat{d} _ {j} < 0 $ であったことになり、$ \hat{S} _ {i} \leqq 0 $ に反する。
したがって、$ \hat{S} _ {i} \leqq \hat{S} _ {N-1} $ も常に成立する。
すなわち、$ l < i < r $ として、任意の $ \hat{d} _ {i} < 0 $ について $ \hat{d} _ {l} , \, \hat{d} _ {r} > 0 $ となる $ l , \, r $ が存在する。
ここで、$ M = \lbrace x \in \hat{D} \mid x < 0 \rbrace $ として、任意の $ \hat{d} _ {i} \in M $ を $ +1 $ する操作を考える。
$ \hat{d} _ {i} < 0 $ かつ転嫁操作をこれ以上行えないことから、$ \hat{S} _ {i} = A _ {2N-1} - A _ {i} $ だったはずであり、$ \hat{S} _ {i} + 1 > A _ {2N-1} - A _ {i} $ となって $ (4) $ を満たさなくなる。
そこで $ \hat{d} _ {l} \in \lbrace P \mid l < i \rbrace $ を満たす $ l $ を選んで、$ \hat{d} _ {l} $ を $ -1 $ する必要がある。
また、$ \hat{d} _ {l} > 0 $ より、$ \hat{d} _ {l} $ から $ \hat{d} _ {l+1} $ への転嫁操作は行われていないのだから、$ \hat{S} _ {l+N} $ の値は変化していない。
$ (6) $ より、$ \hat{S} _ {l+N} = A _ {2N-1} - A _ {l+N} $ なので、こちらも同様に $ \hat{S} _ {l+N} + 1 > A _ {2N-1} - A _ {l+N} $ となって $ (4) $ を満たさなくなり、$ \hat{d} _ {r} \in \lbrace P \mid i < r \rbrace $ となる $ r $ を選んで $ -1 $ する必要がある。
この一連の操作によって、$ \hat{S} _ {N-1} = \sum \hat{d} _ {k} $ の値は $ -1 $ される。
続けて、任意の $ \hat{d} _ {j} \in \lbrace M \mid r < j \rbrace $ を $ +1 $ する操作を考えると、今度は $ \hat{S} _ {j} + 1 = A _ {2N-1} - A _ {j} $ となって $ (4) $ を満たしている。
したがって、$ -1 $ する必要があるのは $ \hat{d} _ {t} \in \lbrace P \mid j < t \rbrace $ となる $ t $ のみである。

これを繰り返すと、長さ $ len $ の操作列 $ \lbrace -1 , \, +1 , \, -1 , \, +1 , \, \ldots , \, -1 \rbrace $ によって、$ \hat{S} _ {N-1} $ の値は $ -1 $ されるとともに、$ \left( \sum _ { x \in P } x \right) $ の値も $ -(len+1) / 2 $ できることがわかる。
$ (7) $ が満たされるまでこの(可変長の)操作列を適用したとき、その操作列の個数だけ $ \hat{S} _ {N-1} $ の値が削られて、$ (5) $ に代入して答えが得られる。
計算量
最も重い処理は $ \lbrace -1 , \, +1 , \, -1 , \, +1 , \, \ldots , \, -1 \rbrace $ の最長操作列を作成・適用する部分である。
操作列を適用した後、$ \hat{d} _ {l} , \, \hat{d} _ {r} \in P $ は存在するが $ \hat{d} _ {i} \in M $ が存在しなくなるという場合、$ -1 $ の操作が $ 1 $ つ余分になって非効率になるし、逆に $ \hat{d} _ {l} , \, \hat{d} _ {r} \in M $ は存在するが $ \hat{d} _ {i} \in P $ が存在しなくなる場合は条件 $ (4) $ を満たさなくなる。
このようなときは $ \hat{d} _ {l} $ と $ \hat{d} _ {r} $ のどちらかを操作列から除外する必要がある。
具体的な実装としては、遅延セグメント木を用いて、
- $ P , \, M $ の連続する区間を併合して $ 1 $ つにする
- セグメント木の偶数番目の要素を $ P $ 、奇数番目の要素を $ M $ に割り当てて構築する
- 以下、条件 $ (4) $ が満たされるまで繰り返す
- 全要素から最小の要素の値だけ減らす(=操作列の適用)
- 値が $ 0 $ になった要素の前後を併合し、不要な部分は無限大に更新する
とすればよい。少し工夫すれば通常のセグメント木でも問題なく、$ O ( N \log N ) $ で実行可能である。
提出コード
atcoder.jp



